1. Introduction
Many people struggle with learning mathematics, which often leads to a general dislike of the subject—myself included. To address this issue, I set out to create a math-based game aimed at improving how students engage with mathematical concepts, particularly those taught at the Hogeschool van Amsterdam (HvA).
Rather than relying on traditional exercises where players answer questions by filling in blanks, this game emphasizes interaction with a virtual world to solve problems. Players must actively apply mathematical concepts to progress—calculating angles, managing resources, or solving puzzles—all embedded within gameplay.
This article explores various mathematical subjects and associated assessments to evaluate whether the game can meaningfully support learning. Each topic is broken down into the specific components a player needs to understand in order to solve related challenges, ensuring that the educational design is both intentional and measurable.
2 Gamification
The core idea behind gamifying math in this project is to place the player directly within a virtual world, where progress depends on solving real mathematical problems. Instead of presenting math as a series of abstract exercises, the game integrates it naturally into the environment—requiring players to engage with mathematical thinking to move forward.
A key design principle was that players should be able to take the corresponding math tests afterwards without struggling with the structure of the questions. To achieve this, no additional formulas or unfamiliar formats were introduced in the puzzles. The way information is presented in the game mirrors how it would appear in a typical test—only distributed across the game world rather than shown all in one place. Players must explore, observe, and piece together the information themselves, reinforcing both understanding and recall.
Each subject area will include a detailed breakdown of how this gamified approach has been applied, explaining how the puzzles align with testable mathematical skills.
The Calculator
One thing that quickly became clear during both testing and development was how crucial it is to have a working, familiar calculator. Expecting players to always have a physical calculator nearby just isn’t realistic — even I, while working on the project, forgot mine several times. This repeated problem didn’t just affect development; it exposed a deeper flaw in the test design itself. The trigonometry challenge I created was originally intended to be solved using a real calculator, and that requirement still holds true in its paper version. So if the game is meant to mirror that experience, the in-game tools need to be just as intuitive and reliable as a physical calculator.
Unfortunately, the Windows Calculator proved to be almost unusable for this. It doesn’t support everything needed, and its interface gives no guidance — nothing that shows how or where to enter a calculation like sin(30) × 10. And since players are often unfamiliar with trigonometry, expecting them to interpret a stripped-down digital tool without any visual feedback creates even more confusion. The experience taught me that without a calculator that looks and works like the real thing, the learning process breaks down.
This realization pushed me to consider more than just function — it became important that the in-game calculator replicate the look and behavior of a standard school calculator. Not only would this reduce confusion, it would help the game serve its original goal: offering a realistic way to practice solving problems like you would in real life. If the test needs a real calculator, the game should feel like it gives you one.
3 Math subjects
In this chapter each subject would be further explored, specifically what the user should learn, and explanations in more simple terms of how to solve equations.
3.1 Trigonomotry
In this module, students are expected to learn:
- How to define and use the sine, cosine, and tangent ratios in a right triangle.
- How to convert between degrees and radians.
- How to write and modify trigonometric function formulas.
- How to differentiate trigonometric functions. This section will explain each of these topics in simple terms, using examples to support understanding.
3.1.1 sine, cosine and tangent
Trigonometry begins with understanding how the sides of a right triangle relate to its angles. The three basic trigonometric ratios are:
- Sine (sin) = opposite / hypotenuse
- Cosine (cos) = adjacent / hypotenuse
- Tangent (tan) = opposite / adjacent These relationships can be remembered using the mnemonic SOH CAH TOA.
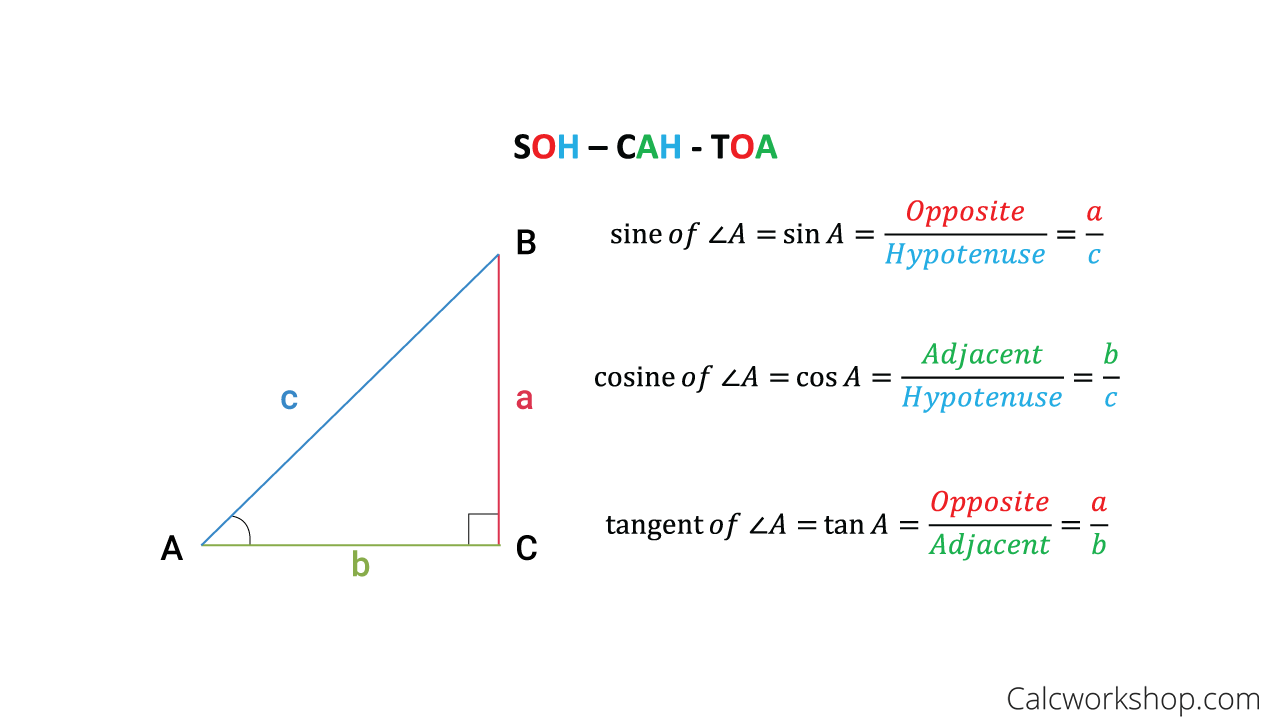
Definitions:
- Opposite: the side opposite the angle you’re looking at.
- Adjacent: the side next to the angle (but not the hypotenuse).
- Hypotenuse: the longest side of the triangle, always opposite the right angle.
Example Problem:
You are given angle α = 30° and the adjacent side = 15 units. You are asked to find the hypotenuse (let’s call it c).
Using cosine, because we know the adjacent and want to find the hypotenuse:
cos(30°) = adjacent / hypotenuse cos(30°) = 15 / c
Now solve for c: c = 15 / cos(30°)
Using a calculator: cos(30°) ≈ 0.866 c = 15 / 0.866 ≈ 17.32 So the hypotenuse is approximately 17.32 units.
Solving for an angle
If you know two sides of the triangle, you can also find the angle. For example, if you know the opposite side and the hypotenuse, use sine: sin(θ) = opposite / hypotenuse θ = sin⁻¹(opposite / hypotenuse)
The sin⁻¹ function is called the inverse sine, and it returns the angle for the given ratio.
3.1.2 Convert Degrees to Radians and vice versa
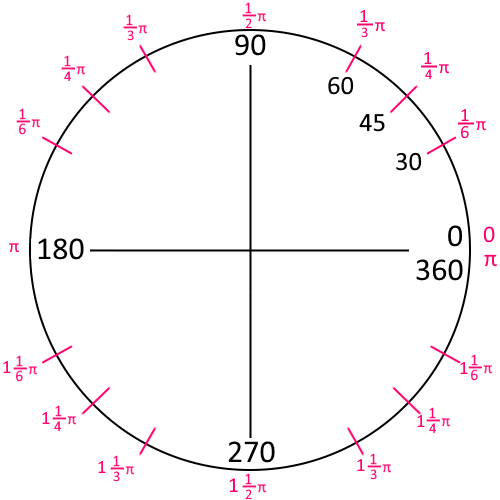 Radians and degrees are both units for measuring angles. Calculators can use either, so it’s important to know how to convert between them. #### Degrees to Radians:
Radians and degrees are both units for measuring angles. Calculators can use either, so it’s important to know how to convert between them. #### Degrees to Radians:To convert degrees into radians, use this formula: radians = degrees × (π / 180)
Example: Convert 20° to radians: radians = 20 × π / 180 ≈ 0.35 radians
Radians to Degrees:
To convert radians back to degrees: degrees = radians × (180 / π)
Example: Convert π/3 radians to degrees: degrees = (π / 3) × 180 / π = 60°
Tip: Always check your calculator’s mode (DEG or RAD) before doing calculations. Wrong mode = wrong result.
3.1.3 Gamification of Trigonomotry
In the game, trigonometry is introduced through a zipline puzzle. The player needs to calculate the correct length of a rope to reach the top of a mountain using a harpoon cannon.
- The game gives the angle (from the harpoon) and the horizontal distance to the mountain.
- The player sees three ropes labeled with different lengths. Only one is correct.
- Ancient glyphs provide the clues (a way to deliver tutorials diegetically).
- As puzzles progress, the player must calculate:
- Unknown sides using SOH CAH TOA.
- Angles using inverse trigonometric functions.
- Problems become more complex over time.
User Testing:
To test whether the trigonometry puzzle would work in practice, I created a physical paper prototype. On a single A4 sheet, I sketched a mountain and placed a small paper wagon with a minifigure at its base. I added three pieces of string to represent possible ropes for the cable system, each a different length. The most important parts of the prototype were two additional sheets: one clearly explained the SOSCASTOA rule (known in English as SOHCAHTOA), and the other contained the actual question. The goal of the test was to ask: “Which rope should you pick?” Participants could use the explanation sheet and the calculator to help figure it out. This setup was intended to simulate how the puzzle might appear in the game, where information is available but needs to be applied correctly.
- Test 1: A user unfamiliar with SOHCAHTOA struggled with brute-forcing answers. Solution: Make wrong ropes reflect plausible errors (e.g., using sine or tangent instead of cosine).
- Test 2: A math-savvy user suggested adding tangent-based puzzles and used a drawing tool to solve the triangle. This inspired adding sketching tools or paper in-game.
- Test 3: Another beginner needed a clearer explanation of the ratios and their use. This led to adding more glyph-based hints in-game.
After the paper prototype, I translated the concept into a Unity demo. In the digital version, a wagon stood at the base of a mountain with a harpoon launcher nearby. Info boards explained the use of SOSCASTOA, and on a table, several ropes were laid out, each marked with its length. This version was tested by two people with no prior experience in trigonometry. Both were able to complete the puzzle with minimal help. The only assistance provided was how to walk around in the scene and how to open the calculator app. Interestingly, using a physical calculator worked better than the Windows one, likely due to its clearer layout. The most important change from the paper to the digital version wasn’t about the objects themselves, but about clarity — the feedback had shown me that players needed more help understanding how to apply SOSCASTOA.

3.2 Not completed subjects
3.2.1 Functions and Graphs
Understanding functions and their graphical representations is fundamental in mathematics. A function describes how one variable depends on another and can be expressed using an equation, a graph, or a table.
- Understand what functions are and be able to manipulate functions:
Learn to recognize functions as relationships between input and output values, and practice operations such as shifting, stretching, reflecting, and combining them. - Understand the relationship between the graph and equation of a linear function:
Explore how changes in the slope and intercept of a linear equation (e.g., y = mx + b) affect its graph, and vice versa. - Understand the relationship between the graph and equation of a fractional linear function:
Analyze functions of the form f(x) = (ax + b)/(cx + d), including their asymptotes, discontinuities, and overall behavior. - Understand the relationship between the graph and equation of a quadratic function:
Study parabolas and how their shape and position change based on the coefficients in equations like y = ax² + bx + c. - Understand the relationship between the graph and equation of a root function:
Learn how functions involving square roots or other roots (e.g., f(x) = √x) are graphed and how to interpret their domains and transformations. - Be able to use graphs to solve equations:
Use intersections, zeros, and graphical analysis to find approximate or exact solutions to equations.
3.2.2 Differentiation 1
Differentiation is the cornerstone of calculus, allowing us to study how functions change.
- Explain what derivatives of functions are for:
Understand that derivatives represent the rate of change or the slope of a function at a given point, with applications in physics, economics, and beyond. - Determine the slope at a certain point on the graph:
Learn to calculate the derivative at a specific x-value to find the instantaneous rate of change or the gradient of the tangent. - Differentiate various functions:
Gain fluency in applying basic differentiation rules to power functions, polynomials, exponential and trigonometric functions. - Apply the product rule:
Use the formula (fg)’ = f’g + fg’ to differentiate the product of two functions. - Apply the quotient rule:
Apply the formula (f/g)’ = (f’g - fg’) / g² to differentiate a quotient of two functions. - Apply the chain rule:
Master the chain rule to differentiate composite functions, expressed as f(g(x)).
3.2.3 Differentiation 2
This section builds on basic differentiation to apply it in practical scenarios.
- Find the tangent of a graph at a specific point:
Use derivatives to write the equation of a line that just touches the graph at a point (i.e., the tangent line). - Find the rise, fall, and extreme values of a function:
Identify where a function increases or decreases and locate its maxima and minima by analyzing the first derivative. - Apply derivatives to solve optimization problems:
Use critical points and second derivative tests to find the optimal values in real-world scenarios (e.g., maximizing area or minimizing cost).
3.2.4 Geometry
This section reinforces classical geometry with a focus on calculation and spatial understanding.
- Calculate one of the unknown sides in a right-angled triangle using the Pythagorean theorem:
Apply the relation a² + b² = c² to find missing side lengths. - Calculate the distance between two points:
Use the distance formula based on the Pythagorean theorem to determine the straight-line distance in coordinate geometry. - Apply sine and cosine rules within any triangle to calculate an unknown side and/or angle:
Use the sine rule (a/sin A = b/sin B = c/sin C) and cosine rule (c² = a² + b² - 2ab cos C) for non-right triangles. - Calculate the distance between a point and a line:
Find the perpendicular distance using algebraic methods and vector projections. - Determine angles (including the smallest angle) between lines using the tangent rule and/or direction coefficient:
Calculate angles based on the slopes or vectors of lines, often involving inverse trigonometric functions.
3.2.5 Probability Theory
This introduces basic probability through hands-on examples and core formulas.
- Calculate probabilities with dice:
Explore outcomes and calculate probabilities in single and multi-dice scenarios using sample spaces. - Calculate probabilities with a vase and marbles:
Practice drawing without replacement and conditional probability using real-world-inspired examples. - Know how to calculate an expected value:
Understand how to compute the average or “expected” result from a random variable or set of outcomes. - Know how to apply permutations and combinations in probability problems:
Learn when and how to count arrangements (permutations) and selections (combinations) to find probabilities in complex situations.
3.2.6 Probability Distributions
This section introduces two key types of probability distributions used in data science and statistics.
- Be familiar with the Normal distribution and be able to perform some calculations:
Understand the bell-shaped curve and use tables or tools to calculate probabilities based on standard deviations from the mean. - Be familiar with the Poisson distribution and be able to perform some calculations:
Learn to model rare events over time or space, using the Poisson formula and interpreting its assumptions and limitations.
Conclusion
Throughout the research conducted for this article, many valuable lessons were learned. One key realization was that teaching new concepts is similar to giving players a tutorial in a game. It is most effective to present information in small, manageable pieces exactly when the learner needs it and can immediately apply the new technique.
Reading numerous math education papers highlighted that overwhelming learners with excessive information—especially in dull or unengaging formats—is one of the least effective ways to teach. However, by embedding new concepts into interactive game mechanics, learners are more likely to retain and understand the material.
From this research and my own struggles with learning math, I concluded that gamification can significantly aid in mastering subjects like mathematics.
Continuation
For further development of this project, I would continue refining the different math subjects and investigate more deeply how players learn most effectively. I plan to consult multiple math teachers to understand the best traditional teaching methods and how students learn in typical classroom settings. Additionally, I would conduct more extensive testing of the game demos with a wider range of participants, varying in age and math experience, to gather diverse feedback and improve the learning experience.